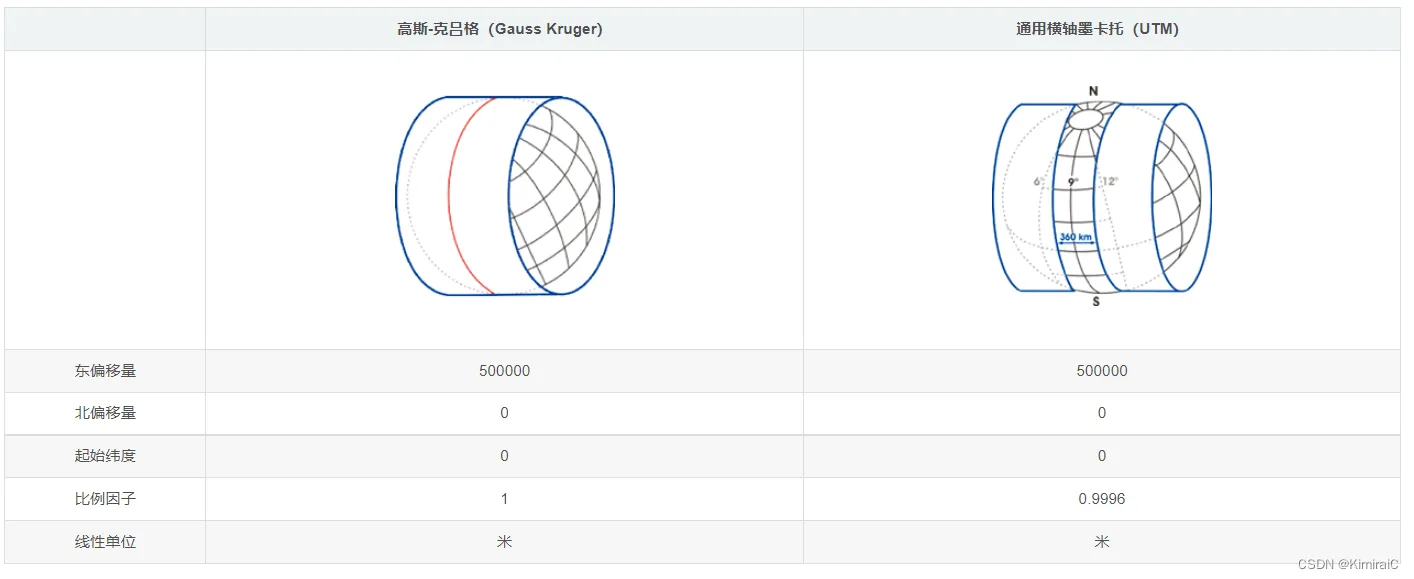
地理坐标系(Geographic Coordinate System, GCS)和投影坐标系(Projected Coordinate System, PCS)是**测绘(Surveying and Mapping)、地理信息系统(Geographic Information System, GIS)、遥感(Remote Sensing, RS)领域的核心坐标体系,二者的本质差异源于地球是不规则椭球面(Irregular Ellipsoidal Earth)与地图/工程应用需要平面(Planar Application)**的核心矛盾(原表述“球面”为简化,地球实际是接近椭球的不规则曲面)。本文从定义、区别、应用、转换四个维度展开深度分析,同步补充全英文专业术语、规范公式、参数实例及实际意义说明。
一、核心定义:球面与平面的本质差异
1. 地理坐标系(GCS, Geographic Coordinate System):球面坐标体系(Spherical Coordinate System)
地理坐标系是基于**地球椭球体(Ellipsoid)的球面坐标系,核心是通过经纬度(Longitude λ, Latitude φ)**描述地表任意点的位置,其本质是对地球不规则曲面的数学近似(Mathematical Approximation),需通过大地基准面将椭球体与地球实际重力面(大地水准面Geoid)拟合。
核心构成要素(Core Components)
| 要素(Component) |
作用(Function) |
典型示例(Typical Examples) |
参数补充与实例 |
| 地球椭球体(Ellipsoid) |
对地球形状的数学抽象,核心参数为长半轴(Semi-major Axis, a)、短半轴(Semi-minor Axis, b)、扁率(Flattening, α)扁率公式: \alpha = \frac{a - b}{a}(实际意义:描述椭球“扁平程度”,值越小越接近正球) |
WGS84椭球(WGS84 Ellipsoid)CGCS2000椭球(CGCS2000 Ellipsoid)克拉索夫斯基椭球(Krasovsky Ellipsoid) |
• WGS84:a=6378137.0\ \text{m},b=6356752.3142\ \text{m},\alpha≈1/298.257223563• CGCS2000:a=6378137.0\ \text{m},b=6356752.3141\ \text{m},\alpha≈1/298.257222101(与WGS84椭球参数几乎一致,仅扁率小数位差异)• 克拉索夫斯基:a=6378245.0\ \text{m},b=6356863.0188\ \text{m},\alpha≈1/298.3 |
| 大地基准面(Datum) |
将椭球体与地球实际表面(Geoid)拟合的参数集,决定椭球的空间位置与姿态(平移、旋转、缩放) |
WGS84基准面(WGS84 Datum, 全球通用)CGCS2000基准面(CGCS2000 Datum, 中国国家基准)北京54基准面(Beijing 54 Datum) |
• WGS84:以地球质心为原点的地心基准面,全球统一拟合• CGCS2000:中国自主地心基准面,覆盖全中国领土,与WGS84在小区域(如单省)转换误差<0.1m• 北京54:参心基准面(以苏联普尔科沃天文台为原点),椭球未与中国大地水准面精准拟合,区域误差可达数米 |
关键特性(Key Characteristics)
- 坐标单位(Coordinate Unit):度(Degree, °),细分可为分(Minute, ′)、秒(Second, ″);
换算关系: 1°=60′,$1′=60″, 1°≈111 \text{km} (赤道处经度1度的地表弧长);
经纬度是角度值,无直接的长度(Length)、面积(Area)度量意义(如纬度30°处,经度1度的弧长≈96.5km,与赤道处差异显著)。
- 空间特性(Spatial Characteristic):椭球面无几何变形(No Distortion on Ellipsoid),但无法直接进行距离、面积的精确计算(度与米的换算需结合具体纬度的曲率半径,如某点纬度φ的子午圈曲率半径M=\frac{a(1-e^2)}{(1-e^2\sin^2φ)^{3/2}},卯酉圈曲率半径N=\frac{a}{(1-e^2\sin^2φ)^{1/2}},其中e为第一偏心率,e=\sqrt{\frac{a^2 - b^2}{a^2}})。
- 全球统一性(Global Uniformity):同一基准面的地理坐标系可覆盖全球,适合跨区域数据整合(Cross-regional Data Integration);但不同基准面的GCS间存在空间偏移(如北京54与CGCS2000在华北地区经纬度偏移约0.001°)。
2. 投影坐标系(PCS, Projected Coordinate System):平面坐标体系(Planar Coordinate System)
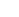
投影坐标系是通过**地图投影(Map Projection)将地理坐标系的椭球面坐标转换为平面直角坐标(Plane Rectangular Coordinate, x, y)**的体系,核心是通过数学算法平衡“球面转平面”的变形问题(Distortion Problem),为工程实践、地图绘制提供线性度量基准(Linear Measurement Benchmark)。
核心构成要素(Core Components)
| 要素(Component) |
作用(Function) |
典型示例(Typical Examples) |
参数补充与实例 |
| 地理坐标系(GCS, 基础) |
投影坐标系的球面基准,所有PCS必须依赖某一GCS存在 |
高斯-克吕格投影基于CGCS2000UTM投影基于WGS84 |
• 中国国家标准:1:1万~1:5万地形图的高斯-克吕格投影强制绑定CGCS2000 GCS• 全球通用:UTM投影默认绑定WGS84 GCS,覆盖除南北极外的全球区域 |
| 投影方法(Projection Method) |
球面转平面的数学算法,决定变形类型(角度/面积/长度优先保留) |
等角投影(Conformal Projection, 墨卡托、高斯-克吕格)等积投影(Equal-area Projection, 阿尔伯斯)任意投影(Arbitrary Projection) |
• 等角投影:保持局部角度不变(如地形图、航海图),但面积变形随纬度增大而加剧(如墨卡托投影中格陵兰岛面积看似与非洲相当,实际仅为非洲1/14)• 等积投影:保持面积不变(如土地利用统计、资源区划图),但角度/形状有轻微变形• 任意投影:无严格变形约束(如旅游地图),兼顾可读性与变形控制 |
| 投影参数(Projection Parameters) |
约束投影的适用区域,控制变形范围与坐标偏移 |
中央经线(Central Meridian)标准纬线(Standard Parallel)坐标偏移量(Coordinate Offset)比例因子(Scale Factor) |
• 中央经线:高斯-克吕格6度带中央经线 \lambda_0=6n-3(n为带号,中国n=13~23),3度带\lambda_0=3n(n=24~45);例:北京(116.4°E)属于3度带n=39,\lambda_0=117°E• 标准纬线:阿尔伯斯投影(中国区域)标准纬线为25°N、47°N,可将中国大部分区域面积变形控制在±0.1%内• 坐标偏移量:高斯-克吕格y轴偏移500km(避免负值),x轴赤道偏移0m(北半球x恒为正);例:某点y=532000m → 实际东向偏移=532000-500000=32000m• 比例因子:高斯-克吕格中央经线比例因子k_0=0.9996(控制中央经线处长度变形<0.04%) |
关键特性(Key Characteristics)
- 坐标单位(Coordinate Unit):米(Meter, m)、千米(Kilometer, km)等线性单位,可直接计算距离、面积、角度;
实例:高斯-克吕格投影下,北京某两点坐标(x_1=4318000\ \text{m}, y_1=532000\ \text{m})、(x_2=4319000\ \text{m}, y_2=532000\ \text{m}),两点距离=1000m(直接差值计算)。
- 空间特性(Spatial Characteristic):必然存在变形(Inevitable Distortion)(角度、面积、长度三者不可兼得);
变形规律:投影区域范围越小,变形越小(如3度带高斯-克吕格投影变形<0.1%,6度带<0.3%);低纬度区域(如赤道)投影变形大于中纬度(如中国华北)。
- 区域局限性(Regional Limitation):同一投影坐标系仅适合特定区域;
实例:UTM投影在高纬度(如60°N以北)长度变形>1%,无法用于高精度测绘;高斯-克吕格投影在南半球需调整x轴偏移规则(避免负值)。
二、核心区别:从基准到应用的全方位对比
| 对比维度(Comparison Dimension) |
地理坐标系(GCS, Geographic Coordinate System) |
投影坐标系(PCS, Projected Coordinate System) |
补充说明 |
| 空间本质(Spatial Essence) |
椭球面坐标系,描述地球表面的球面位置(Spherical Position) |
平面坐标系,描述椭球面投影后的平面位置(Planar Position) |
GCS是对地球的“真实还原”,PCS是“平面化简化” |
| 坐标基准(Coordinate Datum) |
地球椭球体(Ellipsoid)+ 大地基准面(Datum) |
基于某一GCS + 投影方法(Projection Method)+ 投影参数(Projection Parameters) |
PCS的精度完全依赖底层GCS的精度(如基于北京54 GCS的PCS,整体误差>5m) |
| 坐标单位(Coordinate Unit) |
角度单位(Angular Unit:度°、分′、秒″) |
线性单位(Linear Unit:米m、千米km) |
角度转线性需结合曲率半径,线性单位可直接度量 |
| 变形特性(Distortion Characteristic) |
无变形(椭球面本身无几何变形) |
必然变形(角度/面积/长度三选一优先保留) |
等角投影≈“保方向”,等积投影≈“保大小”,无法两全 |
| 度量能力(Measurement Capability) |
无法直接计算距离、面积(需球面三角公式) |
可直接进行线性、面积、角度的精确度量 |
例:GCS计算北京到上海距离需用球面余弦公式,PCS仅需平面两点距离公式 |
| 适用范围(Application Scope) |
全球/跨区域范围(如全球气候研究、GPS定位) |
局部/区域范围(如城市规划、地形图测绘) |
跨区域使用PCS会导致变形失控(如用中国高斯-克吕格投影绘制全球地图,两极变形>100%) |
| 数据关联性(Data Correlation) |
可独立存在,是PCS的基础(Fundamental of PCS) |
必须依赖GCS,无法独立存在(Dependent on GCS) |
仅修改PCS名称但未关联GCS,会导致“伪坐标”(如标注“CGCS2000高斯投影”但实际绑定WGS84 GCS) |
易混淆点澄清(Clarification of Confusing Points)
- 误区1(Misunderstanding 1):WGS84是投影坐标系?
→ 错误(Incorrect)!WGS84是地理坐标系(GCS),UTM/WGS84(Universal Transverse Mercator/WGS84)才是投影坐标系(PCS);
补充:UTM投影将全球分为60个6度带,中国覆盖UTM带号为43~53,每个带的中央经线比例因子k_0=0.9996。
- 误区2(Misunderstanding 2):投影坐标系的变形是误差(Error)?
→ 不是(No)!变形是球面转平面的必然结果(Inevitable Result),投影的核心是按需选择变形类型(Select Distortion Type on Demand);
补充:变形≠误差,误差是“计算错误”,变形是“数学妥协”(如地形图选等角投影保证方向准确,统计地图选等积投影保证面积真实)。
三、典型应用场景:按需选择坐标系
1. 地理坐标系(GCS)的应用场景(Application Scenarios)
GCS的核心优势是全球覆盖(Global Coverage)、无区域限制(No Regional Restriction),适合跨大范围、无需精确线性度量的场景:
- GPS/北斗定位(GPS/BDS Positioning):卫星定位系统直接输出WGS84 GCS经纬度(如北京天安门:116.3975°E,39.9088°N),默认采用WGS84 GCS(全球统一基准,便于跨国家定位);
补充:北斗三号系统可输出CGCS2000 GCS坐标,与WGS84偏差<0.1m,满足国内高精度定位需求。
- 全球遥感数据整合(Global Remote Sensing Data Integration):Landsat、Sentinel卫星原始影像坐标为WGS84 GCS,可直接拼接全球影像(如亚马逊雨林、南极冰盖),无需多次投影转换;
补充:若强行将全球遥感影像转为单一PCS(如UTM),高纬度区域影像会出现严重拉伸变形。
- 跨国家/大洲的GIS分析(Cross-country/Continent GIS Analysis):如全球人口分布、气候变化研究,使用GCS可避免多次投影转换的误差累积(Error Accumulation);
实例:IPCC(政府间气候变化专门委员会)的全球气候模型数据均采用WGS84 GCS,保证跨区域分析的一致性。
- 导航系统的基础坐标(Basic Coordinate of Navigation System):船舶、飞机的导航系统以经纬度为基础坐标,可直接与全球导航地图匹配(Map Matching);
补充:船舶导航最终会将GCS经纬度转换为墨卡托投影PCS(等角),保证航向角计算准确。
2. 投影坐标系(PCS)的应用场景(Application Scenarios)
PCS的核心优势是线性度量能力(Linear Measurement Capability),适合局部区域的精确测绘、工程实践与定量分析:
- 大比例尺地形图测绘(Large-scale Topographic Map Surveying):中国1:1万~1:5万地形图采用高斯-克吕格投影(Gauss-Kruger Projection)(3度带/6度带),等角特性保证地形轮廓、方向关系不畸变;
补充:1:1万地形图强制用3度带(变形<0.1%),1:5万可用6度带(变形<0.3%),满足工程测绘精度要求。
- 城市规划与工程测量(Urban Planning and Engineering Surveying):如道路长度计算、地块面积确权、建筑坐标放样,需使用米制单位的PCS;
实例:北京城建采用CGCS2000高斯-克吕格3度带(中央经线117°E),某地块坐标(x=4318500\ \text{m}, y=532500\ \text{m}),面积可通过x/y坐标直接计算(误差<0.01%)。
- 资源调查与区划(Resource Survey and Zoning):如农田面积统计、森林资源监测,采用等积投影(Equal-area Projection)(如阿尔伯斯投影);
补充:中国全国土地利用调查采用阿尔伯斯等积投影(标准纬线25°N、47°N),全国面积变形<0.1%,保证统计数据准确。
- 航海与航空制图(Marine and Aeronautical Cartography):采用墨卡托投影(Mercator Projection)(等角投影),保证航线方向与实际航向一致;
补充:墨卡托投影中,恒向线(航线)为直线,船员可直接按罗盘航向航行,无需频繁调整角度。
四、坐标系转换:原理、类型与工具
坐标系转换(Coordinate System Transformation)的核心是明确转换的“源”(Source)与“目标”(Target)坐标系参数,转换本质是不同空间基准(Spatial Datum)或不同维度(椭球面/平面)坐标的数学映射(Mathematical Mapping)。根据转换对象不同,分为两大类:地理坐标系间的转换(GCS-GCS Transformation)、地理坐标系与投影坐标系的转换(GCS-PCS Transformation)。
1. 转换的核心前提(Core Premises of Transformation)
无论是哪种转换,必须明确两个关键参数集,否则会导致转换结果错误:
- 源坐标系与目标坐标系的基准面参数(Datum Parameters)(椭球体长半轴a、短半轴b、扁率α,或基准面转换参数ΔX/ΔY/ΔZ/ωx/ωy/ωz/m);
- 若涉及投影转换,需明确投影方法与参数(Projection Method and Parameters)(中央经线、标准纬线、偏移量、比例因子);
补充:仅修改坐标系“名称”未调整坐标值的行为称为“伪转换”(如将“WGS84经纬度”标注为“CGCS2000经纬度”但未做参数转换),会导致数据偏移。
2. 类型一:地理坐标系间的转换(大地基准面转换,Datum Transformation)
适用场景(Application Scenario)
将不同基准面的地理坐标进行转换(如WGS84 GCS转CGCS2000 GCS、北京54 GCS转CGCS2000 GCS),本质是不同椭球面坐标系的空间位置拟合(Spatial Position Fitting)(因不同基准面的椭球体空间位置、姿态不同)。
转换原理与参数(Transformation Principle and Parameters)
核心是通过“平移(Translation)、旋转(Rotation)、缩放(Scaling)”三维空间变换,将源坐标系的大地坐标(经纬度)先转换为空间直角坐标(X,Y,Z),再通过变换公式拟合到目标坐标系的基准面上,最后转回经纬度。
步骤1:经纬度(λ, φ, H)转空间直角坐标(X,Y,Z)
(H为大地高,即点到椭球面的垂直距离,实例中H可取区域平均高程,如华北地区H≈500m)
公式:
\begin{cases}
X = (N + H) \cdot \cosφ \cdot \cosλ \\
Y = (N + H) \cdot \cosφ \cdot \sinλ \\
Z = (N(1 - e^2) + H) \cdot \sinφ
\end{cases}
参数说明与实例:
| 参数 |
符号 |
实际意义 |
实例(北京天安门,WGS84 GCS) |
| 卯酉圈曲率半径 |
N |
该纬度处椭球面的水平曲率半径 |
φ=39.9088°,N≈6378137 / \sqrt{1 - e^2\sin^239.9088°}≈6388946.5\ \text{m} |
| 第一偏心率 |
e |
椭球扁平程度的另一种表达 |
WGS84:e≈0.0818191908 |
| 大地高 |
H |
点到椭球面的垂直距离 |
天安门大地高≈50m |
| 计算结果 |
X,Y,Z |
空间直角坐标(地心为原点) |
X≈4436564.5\ \text{m},Y≈438637.5\ \text{m},Z≈4046567.8\ \text{m} |
步骤2:空间直角坐标的七参数转换
公式:
\begin{bmatrix}
X_{target} \\
Y_{target} \\
Z_{target}
\end{bmatrix}
=
\begin{bmatrix}
X_{source} + ΔX \\
Y_{source} + ΔY \\
Z_{source} + ΔZ
\end{bmatrix}
+
m \cdot
\begin{bmatrix}
0 & -ω_z & ω_y \\
ω_z & 0 & -ω_x \\
-ω_y & ω_x & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
X_{source} \\
Y_{source} \\
Z_{source}
\end{bmatrix}
(注:旋转参数ωx/ωy/ωz以弧度为单位,实际应用中常以“秒”为单位给出,需转换为弧度: 1″≈4.8481368×10^{-6}\ \text{rad})
参数说明与实例(北京54 GCS转CGCS2000 GCS,华北区域):
| 参数 |
符号 |
实际意义 |
实例值 |
| 平移参数(X/Y/Z方向) |
ΔX,ΔY,ΔZ |
源椭球中心相对于目标椭球中心的偏移量 |
ΔX=-5\ \text{m},ΔY=145\ \text{m},ΔZ=85\ \text{m}(X西偏5m,Y北偏145m,Z高偏85m) |
| 旋转参数(绕X/Y/Z轴) |
ω_x,ω_y,ω_z |
源椭球相对于目标椭球的旋转角度 |
ω_x=-0.015″≈-7.27×10^{-8}\ \text{rad},ω_y=-0.018″≈-8.73×10^{-8}\ \text{rad},ω_z=-0.003″≈-1.45×10^{-8}\ \text{rad}(旋转角度极小,仅影响高精度转换) |
| 缩放参数 |
m |
源椭球相对于目标椭球的缩放比例 |
m=0.0000012=1.2×10^{-6}(即缩放1.2ppm,百万分之1.2) |
步骤3:空间直角坐标转回经纬度(逆向公式)
公式(核心步骤):
\begin{cases}
φ = \arctan\left(\frac{Z + e^2 N \sinφ}{r}\right) \quad (迭代计算) \\
λ = \arctan\left(\frac{Y}{X}\right) \\
H = \frac{r}{\cosφ} - N
\end{cases}
(r=\sqrt{X^2 + Y^2},φ需迭代计算至收敛,精度可达 10^{-8^\circ})
三参数与七参数的适用场景对比
| 转换类型 |
参数组成 |
适用场景 |
实例 |
| 三参数转换 |
ΔX,ΔY,ΔZ |
小区域(<100km×100km)、基准面差异小的场景 |
WGS84转CGCS2000(中国大部分区域):ΔX=0,ΔY=0,ΔZ=0(误差<0.1m) |
| 七参数转换 |
ΔX,ΔY,ΔZ,ω_x,ω_y,ω_z,m |
大区域(>100km×100km)、高精度要求的场景 |
北京54转CGCS2000(全国范围):需分区域设置七参数,如华北/华东/华南参数不同 |
3. 类型二:地理坐标系与投影坐标系的转换(投影变换,Projection Transformation)
这是最常用的转换类型,分为正向投影(Forward Projection:GCS→PCS)和逆向投影(Inverse Projection:PCS→GCS),核心是投影公式的正/逆运算。以下以高斯-克吕格投影(中国主流)为例详细说明。
正向投影:经纬度(λ, φ)转平面直角坐标(x, y)
步骤1:确定投影带与中央经线
- 6度带:n = \lfloor \frac{λ + 3}{6} \rfloor,中央经线λ_0=6n-3;
- 3度带:n = \lfloor \frac{λ}{3} \rfloor + 1,中央经线λ_0=3n;
实例:北京(λ=116.4°E)→ 3度带n=39,λ_0=117°E。
步骤2:经纬度归化(将λ, φ转换为相对中央经线的偏移值)
l = λ - λ_0 \quad (l为经度差,以弧度为单位)
实例:l=116.4°-117°=-0.6°≈-0.010472\ \text{rad}。
步骤3:计算子午线弧长X(赤道到该纬度的椭球面弧长)
公式(简化版,适用于WGS84/CGCS2000椭球):
X = a_0φ - a_2\sin2φ + a_4\sin4φ - a_6\sin6φ
其中:
a_0 = a(1 - e^2)(1 + \frac{3e^2}{4} + \frac{45e^4}{64} + \frac{175e^6}{256});
a_2 = a(1 - e^2)(\frac{3e^2}{8} + \frac{45e^4}{128} + \frac{175e^6}{512});
a_4 = a(1 - e^2)(\frac{15e^4}{256} + \frac{525e^6}{4096});
a_6 = a(1 - e^2)(\frac{35e^6}{3072});
实例:北京φ=39.9088°→ X≈4418140.5m(赤道到39.9088°N的子午线弧长)。
步骤4:计算平面直角坐标x, y
\begin{cases}
x = X + \frac{N}{2}\sinφ\cosφ \cdot l^2 + \frac{N}{24}\sinφ\cos^3φ(5 - \tan^2φ + 9η^2 + 4η^4) \cdot l^4 \\
y' = N\cosφ \cdot l + \frac{N}{6}\cos^3φ(1 - \tan^2φ + η^2) \cdot l^3 \\
y = y' + 500000\ \text{m} \quad (y轴偏移,避免负值)
\end{cases}
(η=e'\sinφ,e'为第二偏心率,e'=\sqrt{\frac{a^2 - b^2}{b^2}};\tanφ=\sinφ/\cosφ)
参数实例(北京天安门,CGCS2000 3度带):
| 参数 |
计算值 |
实际意义 |
| x |
≈4418145.2m |
平面直角坐标x(北向),相对于赤道的偏移 |
| y' |
≈-32000.5m |
未偏移的y坐标(西向32000.5m) |
| y |
≈500000 - 32000.5 = 467999.5m |
偏移后的y坐标(东向基准500km) |
逆向投影:平面直角坐标(x, y)转经纬度(λ, φ)
核心是正向公式的逆运算,步骤如下:
- 反向偏移:y' = y - 500000\ \text{m}(还原真实横向偏移);
- 迭代计算:根据x值反推纬度φ(通过子午线弧长公式逆运算);
- 计算经度差l:l = \frac{y'}{N\cosφ} - \frac{y'^3}{6N^3\cos^3φ}(1 - \tan^2φ + η^2);
- 还原经度:λ = λ_0 + l;
- 验证修正:检查φ/λ是否在投影带范围内(如3度带λ∈[λ0-1.5°, λ0+1.5°]),修正计算误差。
实例:已知北京某点PCS坐标(x=4418145.2m,y=467999.5m)→ 逆向计算得λ=116.4°E,φ=39.9088°N(与原GCS坐标一致)。
4. 常用转换工具与方法(Common Transformation Tools and Methods)
| 工具类型(Tool Type) |
典型工具(Typical Tools) |
适用场景(Application Scenarios) |
核心优势(Core Advantages) |
参数补充 |
| 专业GIS软件(Professional GIS Software) |
ArcGIS、QGIS(开源)、SuperMap |
批量GIS数据转换(如shp、tiff、gdb格式),自定义投影参数 |
支持多种坐标系与投影类型,可视化操作,精度可控 |
• ArcGIS:可自定义七参数/三参数,支持“地理变换”(Geographic Transformation)如“WGS_1984_To_CGCS2000_1”• QGIS:集成Proj4库,可直接输入投影参数字符串(如“+proj=gk +zone=39 +datum=CGCS2000 +units=m”) |
| 坐标转换软件(Coordinate Transformation Software) |
CoordMG、高斯投影计算工具、COORD |
单点/小批量坐标转换,测绘人员现场计算与验证 |
轻量高效,操作简单,支持手动输入参数计算 |
• CoordMG:支持高斯-克吕格3/6度带正反算,可导入七参数文件• 高斯投影计算工具:实时显示每一步计算结果,便于验证参数正确性 |
| 在线转换工具(Online Transformation Tools) |
天地图坐标转换API(Tianditu Coordinate Transformation API)、GPS在线转换平台 |
快速验证转换结果,非专业用户临时使用 |
无需安装软件,随时随地可用,支持常用坐标系转换 |
• 天地图API:支持WGS84→GCJ02(高德/百度地图加密坐标)→CGCS2000转换,接口参数需传入经纬度/平面坐标、转换类型 |
| 编程接口(Programming Interfaces) |
Proj4(开源投影库)、GDAL/OGR、ArcPy |
批量自动化转换,开发人员集成到GIS系统中 |
高度自定义,支持大规模数据批量处理,适配系统开发需求 |
• Proj4:投影参数字符串示例(CGCS2000 3度带39带):“+proj=gk +lat_0=0 +lon_0=117 +k=1 +x_0=500000 +y_0=0 +ellps=cgcs2000 +units=m +no_defs” |
五、总结:坐标系的选择与转换原则
-
选择原则(Selection Principle):
- 大范围(全球/全国)、跨区域分析→用GCS(如WGS84/CGCS2000);
- 小范围(城市/县域)、工程度量→用PCS(如高斯-克吕格/UTM);
- 数据整合→优先用GCS(避免多次投影变形),数据应用→优先用PCS(便于度量);
核心:匹配应用场景的空间范围与度量需求,避免因坐标系选择不当导致分析误差(如用UTM投影绘制北极地图,变形>100%)。
-
转换原则(Transformation Principle):
① 优先明确源/目标坐标系的基准面参数,杜绝“伪转换”;
② 大区域(>100km)、高精度(<0.1m)→七参数转换;小区域、低精度→三参数转换;
③ 投影类型匹配场景:等角→地形图/导航,等积→面积统计,任意→一般制图;
④ 转换后需验证:用已知控制点(如GPS控制点)检查转换误差(误差>1m需重新核对参数)。
-
核心关系(Core Relationship):
PCS是GCS的平面化表达(Planar Expression of GCS),GCS是PCS的球面基础(Spherical Foundation of PCS),二者共同构成了地表空间定位(Spatial Positioning)的完整技术体系,支撑测绘、GIS、遥感等领域的各类应用。
附录:常用英文术语对照表(Appendix: Common English Terminology Comparison Table)
| 中文术语(Chinese Terminology) |
英文术语(English Terminology) |
缩写(Abbreviation) |
补充说明 |
| 地理坐标系 |
Geographic Coordinate System |
GCS |
核心为经纬度,基于椭球面 |
| 投影坐标系 |
Projected Coordinate System |
PCS |
核心为平面直角坐标,基于投影算法 |
| 地球椭球体 |
Ellipsoid |
- |
数学抽象,含长半轴/短半轴/扁率参数 |
| 大地基准面 |
Datum |
- |
椭球与地球实际表面的拟合参数集 |
| 经纬度 |
Longitude and Latitude |
λ, φ |
λ(经度):东西向,φ(纬度):南北向 |
| 平面直角坐标 |
Plane Rectangular Coordinate |
x, y |
x:北向,y:东向(高斯-克吕格) |
| 地图投影 |
Map Projection |
- |
球面转平面的数学算法 |
| 等角投影 |
Conformal Projection |
- |
保角度,变形:面积>长度>角度 |
| 等积投影 |
Equal-area Projection |
- |
保面积,变形:角度>长度>面积 |
| 高斯-克吕格投影 |
Gauss-Kruger Projection |
- |
中国主流等角投影,3/6度带划分 |
| 墨卡托投影 |
Mercator Projection |
- |
航海常用等角投影,高纬度变形大 |
| UTM投影 |
Universal Transverse Mercator Projection |
UTM |
全球60个6度带,比例因子0.9996 |
| 中央经线 |
Central Meridian |
λ₀ |
投影带的中心经线,控制变形范围 |
| 标准纬线 |
Standard Parallel |
φ₀ |
等积投影的基准纬线,减小面积变形 |
| 三参数转换 |
Three-Parameter Transformation |
- |
仅平移(ΔX,ΔY,ΔZ),小区域适用 |
| 七参数转换 |
Seven-Parameter Transformation |
- |
平移+旋转+缩放,大区域高精度适用 |
| 空间直角坐标 |
Spatial Rectangular Coordinate |
X,Y,Z |
地心为原点的三维直角坐标 |
| 大地高 |
Geodetic Height |
H |
点到椭球面的垂直距离 |
| 第一偏心率 |
First Eccentricity |
e |
椭球扁平程度参数,e=\sqrt{(a²-b²)/a²} |
| 地理信息系统 |
Geographic Information System |
GIS |
坐标系应用的核心平台 |
| 遥感 |
Remote Sensing |
RS |
多采用GCS进行数据整合 |
注:本文补充的参数实例均为华北地区(北京)典型值,不同区域(如华南、西北)的转换参数需以当地测绘部门发布的官方参数为准;公式均基于WGS84/CGCS2000椭球推导,适配中国主流坐标系应用场景。
 /1
/1