一文讲透测绘坐标系统与投影理论

目录

1. 引言
2. 坐标系统基础理论
   2.1 大地坐标系统
   2.2 平面直角坐标系统
   2.3 高程系统
3. 地图投影核心理论
   3.1 地图投影基本概念
   3.2 投影变形分析
   3.3 投影分类
4. 我国常用坐标系统与投影方法
   4.1 高斯-克吕格投影（核心重点）
   4.2 UTM投影
5. 关键公式与参数解析
6. 实际操作案例
7. 坐标系统与投影的应用原则
8. 总结

1. 引言

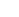
坐标系统是确定地面点空间位置的基准框架，地图投影则是解决球面坐标（大地坐标）向平面坐标转换的核心技术，二者共同构成测绘工作的基础。所有测量数据采集、地形图绘制、工程放样等工作，均需基于统一的坐标系统与投影规则，否则会产生无法预估的位置偏差。

2. 坐标系统基础理论

坐标系统分为空间坐标系统（描述点的三维位置）和平面坐标系统（描述点的二维位置），其中空间坐标系统包含大地坐标系统和高程系统两个维度。

2.1 大地坐标系统

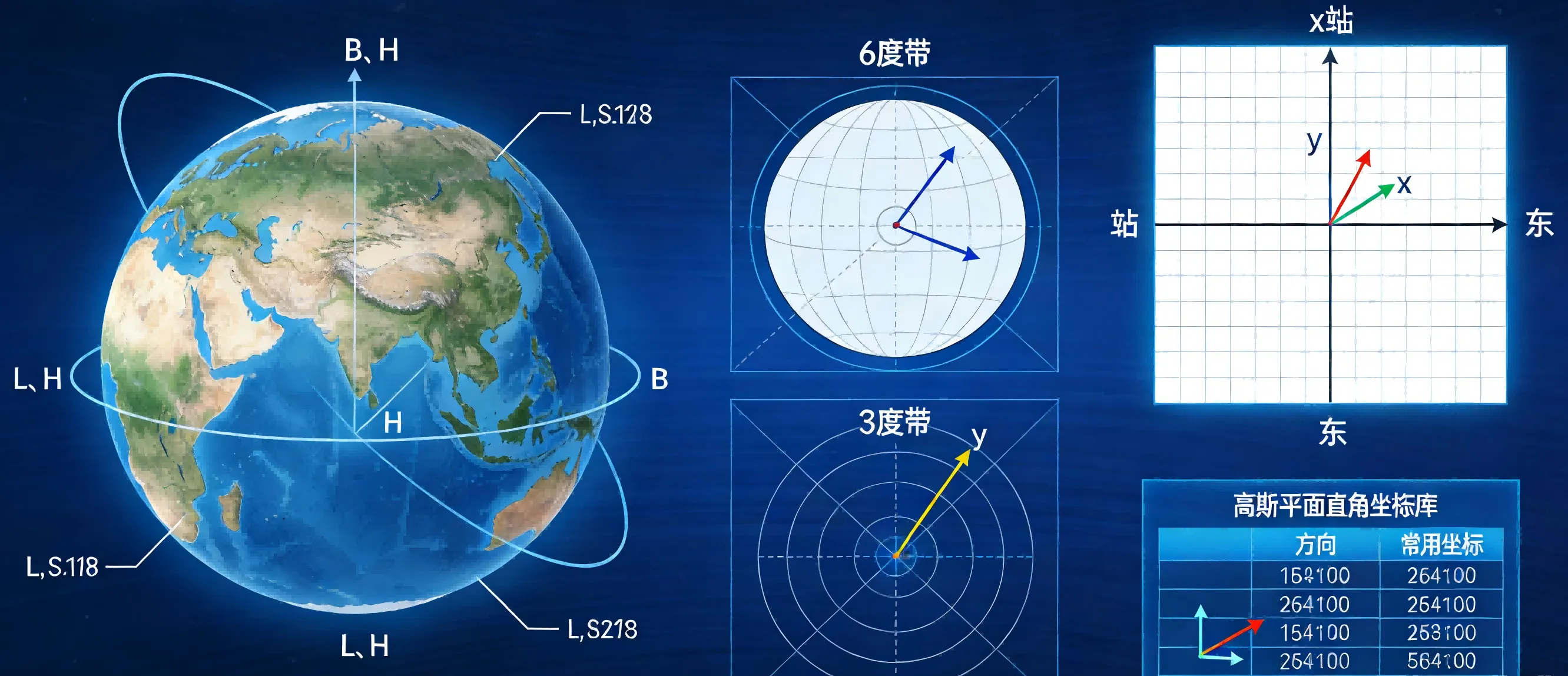
大地坐标系统以地球椭球为基准，用 大地纬度（B）、大地经度（L）、大地高（H） 描述地面点的三维空间位置，简称 BLH 坐标系。

2.1.1 核心概念

• 地球椭球：对地球形状的数学近似，由长半轴 a、短半轴 b、扁率 \alpha=\frac{a-b}{a} 三个关键参数定义。不同椭球对应不同坐标系，如 WGS-84 椭球、CGCS2000 椭球。
• 大地纬度 B：地面点椭球法线与赤道面的夹角，北半球为正，取值范围 0^\circ\sim90^\circ。
• 大地经度 L：地面点椭球子午面与本初子午面（格林尼治子午面）的夹角，东经为正，西经为负，取值范围 -180^\circ\sim180^\circ。
• 大地高 H：地面点沿椭球法线到椭球面的距离，与高程系统的基准面不同。

2.1.2 分类及典型案例

分类	定义	典型坐标系	适用场景
地心大地坐标系	椭球中心与地球质心重合	1. WGS-84坐标系（全球定位系统GPS专用）2. CGCS2000坐标系（我国现行国家大地坐标系）	全球范围测量、卫星导航定位、跨区域测绘工程
参心大地坐标系	椭球中心不与地球质心重合，仅与局部区域大地水准面最佳拟合	1. 1954北京坐标系（采用克拉索夫斯基椭球）2. 1980西安坐标系（采用IAG75椭球）	2000年前我国区域性测绘、小范围工程测量

2.1.3 实际应用要点

• 目前我国所有法定测绘成果均需转换至 CGCS2000 坐标系，1954北京坐标系、1980西安坐标系成果需通过坐标转换模型（如布尔莎模型）完成更新。
• GPS/北斗接收机直接输出的坐标为 WGS-84 坐标系，在我国境内使用时，需通过坐标转换参数转换为 CGCS2000 坐标系（二者椭球参数几乎一致，转换误差可忽略）。

2.2 平面直角坐标系统

大地坐标是球面坐标，无法直接用于平面地形图绘制和工程放样，需通过地图投影转换为平面直角坐标，用 平面直角坐标（x,y） 描述点的二维位置。

2.2.1 核心规则

• 平面直角坐标的 x 轴为纵轴，指向北方向；y 轴为横轴，指向东方向（与数学直角坐标系相反，便于与方位角对应）。
• 原点一般选在投影带的中央子午线与赤道的交点，确保投影区域内坐标为正值。

2.2.2 两类平面直角坐标

类型	定义	适用场景
高斯平面直角坐标	基于高斯-克吕格投影的国家统一平面坐标	全国范围内地形图绘制、跨区域工程测量
独立平面直角坐标	自定义原点和轴向的局部平面坐标	小范围建筑工地、厂区、校园的施工放样（面积小于 $10\ \text{km}^2$ 时，投影变形可忽略）

2.3 高程系统

高程系统描述地面点的垂直位置，核心是确定基准面，分为绝对高程和相对高程。

2.3.1 核心概念

概念	定义	关键作用
大地水准面	平均海水面延伸至大陆内部形成的闭合曲面，是绝对高程的基准面，处处与重力方向垂直	作为高程测量的天然基准
似大地水准面	为弥补大地水准面不规则的缺陷，用于计算正常高的基准面，与大地水准面的差距称为高程异常 \zeta	我国高程系统采用正常高，通过似大地水准面衔接大地高与正常高
绝对高程（海拔）	地面点沿铅垂线到大地水准面的距离，记为 H	法定高程数据的基准
相对高程	地面点沿铅垂线到任意假定水准面的距离	局部工程测量（如基坑深度测量）
高差 h	两点绝对高程之差，h_{AB}=H_B-H_A	水准测量的核心观测值，正负号表示坡度方向（正为上坡，负为下坡）

2.3.2 我国现行高程基准

• 1985国家高程基准：以青岛验潮站1952-1979年的潮汐观测资料计算的平均海水面为基准，替代了1956年黄海高程基准。

• 大地高 H 与正常高 H_{正常} 的换算公式：

  H_{正常}=H-\zeta

  参数说明：

  • \zeta：高程异常，单位为米（m）；CGCS2000 坐标系下，我国通过 似大地水准面精化模型 可查询任意点的 \zeta 值。

2.3.3 实际应用案例

已知 A 点绝对高程 H_A=100.000\ \text{m}，水准测量测得 AB 高差 h_{AB}=+2.567\ \text{m}，则 B 点绝对高程：

H_B=H_A+h_{AB}=100.000+2.567=102.567\ \text{m}

若 B 点处高程异常 \zeta=0.123\ \text{m}，则 B 点大地高：

H=H_{正常}+\zeta=102.567+0.123=102.690\ \text{m}

3. 地图投影核心理论

地球是不可展的曲面，将其投影到平面上必然产生变形，地图投影的本质是通过数学模型平衡变形，满足不同测绘需求。

3.1 地图投影基本概念

地图投影是将地球椭球面上的点（B,L），通过数学函数关系转换为平面上的点（x,y）的过程，数学表达式为：

\begin{cases}x=f_1(B,L)\\y=f_2(B,L)\end{cases}

其中 f_1、f_2 为投影函数，不同投影的函数形式不同。

3.2 投影变形分析

投影变形分为 长度变形、角度变形、面积变形，三者无法同时消除，需根据用途选择变形类型。

变形类型	定义	实际影响
长度变形	投影后线段长度与椭球面原长的比值，记为 V_s=\frac{s'-s}{s}	影响距离测量精度，变形过大时无法直接用于工程放样
角度变形	投影后角度与椭球面原角度的差值	影响地物形状的相似性，角度变形为0时称为等角投影
面积变形	投影后图形面积与椭球面原面积的比值，记为 V_P=\frac{P'-P}{P}	影响面积量算精度，面积变形为0时称为等积投影

3.3 投影分类

3.3.1 按变形性质分类（核心分类）

投影类型	变形特点	适用场景
等角投影（正形投影）	角度变形为0，长度和面积存在变形	地形图绘制、工程测量、导航定位（高斯-克吕格投影属于此类）
等积投影	面积变形为0，角度和长度存在变形	行政区划图、土地利用图等需要面积量算的地图
任意投影	长度、角度、面积均有变形，变形程度介于等角与等积之间	小比例尺普通地图（如世界地图）

3.3.2 按投影面分类

投影类型	投影面形状	典型代表
方位投影	平面	极地地区地图
圆柱投影	圆柱面	墨卡托投影（航海地图）
圆锥投影	圆锥面	中纬度地区小比例尺地图

4. 我国常用坐标系统与投影方法

4.1 高斯-克吕格投影（我国核心投影方法）

高斯-克吕格投影是 横切椭圆柱等角投影，是我国大比例尺地形图（1:1万、1:2.5万、1:5万、1:10万）的法定投影方法。

4.1.1 投影原理

1. 将一椭圆柱横套在地球椭球外，使椭圆柱的轴线与椭球赤道面重合，椭圆柱的母线与椭球中央子午线相切。
2. 中央子午线上的点投影到椭圆柱上后长度不变（长度变形为0）。
3. 将椭圆柱沿母线展开为平面，即得到高斯平面直角坐标系。

4.1.2 分带投影规则（核心：控制长度变形）

由于离中央子午线越远，长度变形越大，因此采用分带投影，我国分为 6度带 和 3度带 两种分带方式。

1. 6度带（适用于1:2.5万~1:10万地形图）

   • 带号范围：全球共分60个带，带号 n=1\sim60。

   • 中央子午线经度公式：L_0=6n-3

   • 带号计算公式：n=\lfloor\frac{L+3}{6}\rfloor
     参数说明：

     • L_0：中央子午线经度（°）；
     • n：6度带带号（正整数）；
     • L：待求点大地经度（°）；
     • \lfloor\cdot\rfloor：向下取整函数（取不大于括号内数值的最大整数）。

   • 分带范围：

   • 第1带中央子午线 L_0=3^\circ，覆盖经度范围 $0^\circ\sim6^\circ；第2带 L_0=9^\circ，覆盖 6^\circ\sim12^\circ，以此类推。

2. 3度带（适用于1:1万及更大比例尺地形图）

   • 带号范围：全球共分120个带，带号 n=1\sim120。
   • 中央子午线经度公式：L_0=3n
   • 带号计算公式：n=\lfloor\frac{L-1.5}{3}\rfloor+1 或 n=\lceil\frac{L}{3}\rceil
     参数说明：
     • \lceil\cdot\rceil：向上取整函数（取不小于括号内数值的最小整数）；
     • 其他参数同6度带。
   • 分带范围：第1带中央子午线 L_0=3^\circ，覆盖 1.5^\circ\sim4.5^\circ；
     第2带 L_0=6^\circ，覆盖 4.5^\circ\sim7.5^\circ，以此类推。

4.1.3 高斯平面坐标的 y 轴坐标处理

高斯投影中，中央子午线东侧 y 坐标为正，西侧为负，为避免负坐标，规定将每带的 y 坐标值加上 500000 m；同时为区分带号，在 y 坐标前加带号，最终形成通用坐标格式：

y_{通用}=带号 + (y_{自然}+500000)

示例：某点3度带带号为37，自然坐标 y_{自然}=-12345.678\ \text{m}，则通用坐标：

y_{通用}=37+( -12345.678+500000 )=37\ 487\ 654.322\ \text{m}

4.2 UTM投影

UTM投影是 横轴等角割圆柱投影，与高斯-克吕格投影类似，区别在于椭圆柱与地球椭球相割而非相切，中央子午线长度变形为 -0.000001（约百万分之一），变形分布更均匀。

• 分带方式：6度带，全球共60个带，带号 1\sim60。
• 适用场景：全球范围的卫星影像地图、小比例尺工程测量，我国部分涉外工程会采用UTM投影。

5. 关键公式与参数解析

公式名称	公式表达式	参数含义	应用场景
6度带中央子午线经度	L_0=6n-3	L_0：中央子午线经度（°）；n：6度带带号	计算6度带投影的中央子午线
6度带带号	n=\lfloor\frac{L+3}{6}\rfloor	L：待求点大地经度（°）；\lfloor\cdot\rfloor：向下取整	由大地经度确定6度带带号
3度带中央子午线经度	L_0=3n	L_0：中央子午线经度（°）；n：3度带带号	计算3度带投影的中央子午线
3度带带号	n=\lceil\frac{L}{3}\rceil	L：待求点大地经度（°）；\lceil\cdot\rceil：向上取整	由大地经度确定3度带带号
高斯通用 y 坐标	y_{通用}=带号 + (y_{自然}+500000)	y_{自然}：高斯自然坐标（m）；500000m：偏移量	避免 y 坐标为负，区分投影带
大地高与正常高换算	H_{正常}=H-\zeta	H：大地高（m）；\zeta：高程异常（m）；H_{正常}：正常高（m）	GPS高程与水准高程的衔接

6. 实际操作案例

案例1：由大地经度计算投影带号及中央子午线

已知条件：某点大地坐标为北纬 34^\circ25'，东经 L=108^\circ30'=108.5^\circ。
需求：计算该点的6度带、3度带带号及中央子午线经度。

计算过程

1. 6度带计算

   • 带号：n=\lfloor\frac{108.5+3}{6}\rfloor=\lfloor\frac{111.5}{6}\rfloor=\lfloor18.583\rfloor=18
   • 中央子午线：L_0=6\times18-3=105^\circ
   • 结论：该点位于6度带第18带，中央子午线 105^\circ。

2. 3度带计算

   • 带号：n=\lceil\frac{108.5}{3}\rceil=\lceil36.167\rceil=37
   • 中央子午线：L_0=3\times37=111^\circ
   • 结论：该点位于3度带第37带，中央子午线 111^\circ。

案例2：高斯平面坐标转换（软件操作）

需求：将GPS测得的WGS-84大地坐标（B=34^\circ25'00''，L=108^\circ30'00''，H=500.000\ \text{m}）转换为CGCS2000 3度带高斯平面坐标。
操作工具：南方CASS 10.0（测绘常用成图软件）
操作步骤

1. 打开软件，进入【坐标转换】模块，选择坐标系类型：源坐标系为WGS-84，目标坐标系为CGCS2000 3度带。
2. 输入待转换点的大地坐标（B,L,H），根据案例1结果，选择3度带带号37，中央子午线 111^\circ。
3. 点击【转换】，软件自动计算高斯平面坐标，输出结果示例：x=3792567.890\ \text{m}，y=37\ 486\ 234.567\ \text{m}。
4. 精度验证：通过水准测量测得该点正常高 H_{正常}=499.877\ \text{m}，查询当地似大地水准面模型得 \zeta=0.123\ \text{m}，则大地高 H=H_{正常}+\zeta=499.877+0.123=500.000\ \text{m}，与GPS测量值一致，转换精度合格。

案例3：独立平面直角坐标的工程应用

需求：某建筑工地范围约 1\ \text{km}\times1 \text{km}，需建立独立平面直角坐标系统用于施工放样。
操作步骤

1. 选择工地西南角为坐标原点 O(0,0)。
2. 定义 x 轴指向正北方向，y 轴指向正东方向。
3. 使用全站仪测量工地内某控制点 A 的坐标，测得 A 点相对于原点的北距为 250.000\ \text{m}，东距为 300.000\ \text{m}，则 A 点独立坐标为 A(250.000, 300.000)。
4. 放样应用：根据设计图纸，建筑物角点 B 的设计坐标为 (150.000, 200.000)，使用全站仪在 A 点设站，输入 A、B 坐标，直接放样出 B 点实地位置。
   核心优势：小范围独立坐标系无需考虑投影变形，操作简便，放样精度满足施工要求。

7. 坐标系统与投影的应用原则

1. 统一性原则：同一测绘项目必须采用同一坐标系和投影方法，避免数据冲突。
2. 精度匹配原则：大比例尺地形图（1:1万及以上）用3度带高斯投影，小比例尺用6度带；工程放样优先采用国家统一坐标系，小范围可采用独立坐标系。
3. 更新换代原则：逐步淘汰1954北京坐标系、1980西安坐标系，转换为CGCS2000坐标系，确保成果合法性。
4. 高程衔接原则：GPS测量的大地高需通过高程异常转换为正常高，才能与水准测量成果衔接。

8. 总结

坐标系统与投影理论是测绘工作的“语言”，大地坐标系统确定空间位置基准，地图投影解决球面到平面的转换，高程系统描述垂直位置。掌握高斯-克吕格投影的分带规则、坐标转换方法，是开展地形图绘制、工程放样、卫星定位等工作的核心技能。在实际应用中，需根据项目范围、精度要求选择合适的坐标系和投影方法，确保测绘成果的准确性和统一性。

❓ 有没有小伙伴试过这个？效果怎么样呀