数学第一章：认识数学符号⑦-专业辅助符号

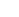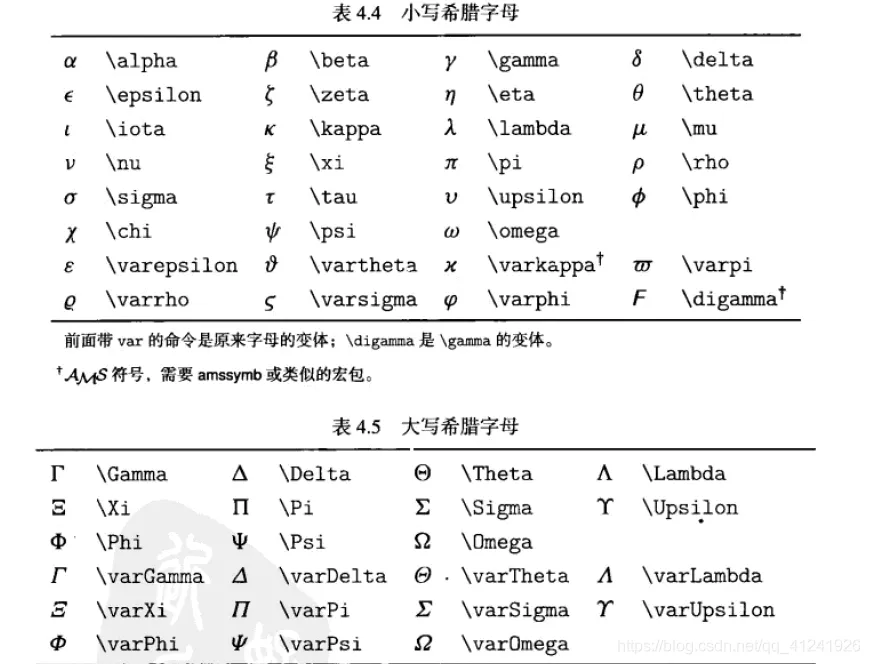
一、 集合与逻辑辅助符号

这类符号用于精简集合描述、明确逻辑关系，是各分支通用的“书写工具”。

符号	数学意义	实用举例	读音（中文+英文常用念法）
I_A(x)（或\chi_A(x)）	指示函数（特征函数）：x\in A时为1，否则为0	A=\{1,2,3\}，则I_A(2)=1，I_A(4)=0；积分\int_{\mathbb{R}}I_{[0,1]}(x)dx=1	中文：集合A的指示函数英文：indicator function of A / characteristic function of A
\exists!	唯一存在量词：“存在唯一的”	\exists!x\in\mathbb{R}，使得$2x=4（唯一解x=2）；\exists!素数p为偶数（p=2$）	中文：存在唯一英文：there exists uniquely
\forall	全称量词：“对所有的”（逻辑核心辅助符号）	\forall x\in\mathbb{R}，x^2\geq0；\forall n\in\mathbb{N}，n+1>n	中文：对任意 / 对所有英文：for all / for every
\implies（或\rightarrow）	逻辑蕴含：“若…则…”	x>3\implies x>2；n为偶数\implies n^2为偶数	中文：蕴含 / 推出英文：implies / if...then...
\iff（或\leftrightarrow）	逻辑等价：“当且仅当”	x^2=1\iff x=1或x=-1；A\subseteq B\iff\forall x\in A,x\in B	中文：等价于 / 当且仅当英文：if and only if (iff) / is equivalent to
\triangleq（或\stackrel{\text{def}}{=}）	定义符号：“记作”“定义为”	定义f(x)\triangleq x^2+1；\mathbb{N}^*\triangleq\mathbb{N}\setminus\{0\}（正自然数集）	中文：定义为英文：defined as / denotes

二、 分析辅助符号

用于极限、积分、函数性质描述，简化分析领域的复杂推导过程。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\text{sgn}(x)	符号函数：x>0时为1，x=0时为0，x<0时为-1	\text{sgn}(3)=1，\text{sgn}(-2)=-1；$	x
\lfloor x\rfloor	下取整函数（地板函数）：不大于x的最大整数	\lfloor 2.3\rfloor=2，\lfloor -1.5\rfloor=-2；\lfloor\pi\rfloor=3	中文：x的下取整 / 地板函数x英文：floor function of x
\lceil x\rceil	上取整函数（天花板函数）：不小于x的最小整数	\lceil 2.3\rceil=3，\lceil -1.5\rceil=-1；\lceil\sqrt{2}\rceil=2	中文：x的上取整 / 天花板函数x英文：ceiling function of x
o(g(x))（小o）	高阶无穷小：\lim\frac{f(x)}{g(x)}=0（x\to a）	x\to0时，x^2=o(x)；n\to\infty时，\ln n=o(n)	中文：小o of g(x)英文：little o of g(x)
O(g(x))（大O）	同阶无穷小：\exists M>0，$	f(x)	\leq M
\sim g(x)（渐近等价）	等价无穷小/渐近等价：\lim\frac{f(x)}{g(x)}=1（x\to a）	x\to0时，\sin x\sim x；n\to\infty时，n+\sqrt{n}\sim n	中文：渐近等价于g(x)英文：asymptotic to g(x)
\Gamma(z)	伽马函数（阶乘推广）：\Gamma(z)=\int_0^{+\infty}t^{z-1}e^{-t}dt（\text{Re}(z)>0）	\Gamma(n)=(n-1)!（n\in\mathbb{N}^*）；\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}	中文：伽马函数z英文：gamma function of z
B(p,q)	贝塔函数（与伽马函数相关）：B(p,q)=\int_0^1t^{p-1}(1-t)^{q-1}dt	B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}；B(2,3)=\frac{1}{12}	中文：贝塔函数(p,q)英文：beta function of (p,q)
u(x)（或\theta(x)）	单位阶跃函数：x>0时为1，x<0时为0，x=0时为\frac{1}{2}（或1）	电路中电压突变：u(t-1)（t=1时阶跃）；\delta(x)=\frac{du(x)}{dx}（广义导数）	中文：单位阶跃函数英文：unit step function / Heaviside step function

三、 代数与线性代数辅助符号

用于矩阵、向量、张量运算及代数结构描述，简化线性变换、方程求解的表达。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\delta_{ij}	克罗内克符号：i=j时为1，i\neq j时为0	单位矩阵\mathbf{I}=(\delta_{ij})；\sum_{i=1}^n\delta_{ij}=1	中文：克罗内克delta ij英文：Kronecker delta ij
\epsilon_{ijk}	列维-奇维塔符号（克朗巴符号）：偶排列为1，奇排列为-1，重复指标为0	向量叉积(\vec{a}\times\vec{b})_k=\sum_{i,j}\epsilon_{ijk}a_ib_j；行列式\det(\mathbf{A})=\sum_{i,j,k}\epsilon_{ijk}A_{i1}A_{j2}A_{k3}	中文：列维-奇维塔epsilon ijk英文：Levi-Civita epsilon ijk
\otimes	张量积（外积）：向量/矩阵/张量的扩展运算	向量\vec{a}\otimes\vec{b}为二阶张量；矩阵\mathbf{A}\otimes\mathbf{B}（ Kronecker 积）：\begin{pmatrix}1&2\\3&4\end{pmatrix}\otimes\begin{pmatrix}a&b\\c&d\end{pmatrix}=\begin{pmatrix}a&b&2a&2b\\c&d&2c&2d\\3a&3b&4a&4b\\3c&3d&4c&4d\end{pmatrix}	中文：张量积 / 克罗内克积英文：tensor product / Kronecker product
\odot	哈达玛积（element-wise积）：矩阵对应元素相乘	\begin{pmatrix}1&2\\3&4\end{pmatrix}\odot\begin{pmatrix}a&b\\c&d\end{pmatrix}=\begin{pmatrix}a&2b\\3c&4d\end{pmatrix}	中文：哈达玛积英文：Hadamard product
\text{tr}(\mathbf{A})	矩阵的迹：主对角线元素之和	\text{tr}\begin{pmatrix}1&2\\3&4\end{pmatrix}=1+4=5；\text{tr}(\mathbf{AB})=\text{tr}(\mathbf{BA})	中文：矩阵A的迹英文：trace of matrix A
\text{rank}(\mathbf{A})（或\rho(\mathbf{A})）	矩阵的秩：最高非零子式的阶数	\text{rank}\begin{pmatrix}1&2&3\\2&4&6\end{pmatrix}=1；可逆矩阵\text{rank}(\mathbf{A})=n（n为阶数）	中文：矩阵A的秩英文：rank of matrix A
\ker(f)	线性映射的核（零空间）：f(x)=0的解集合	线性变换f(x)=Ax，\ker(f)=\{x\mid Ax=0\}；\dim\ker(f)+\dim\text{im}(f)=\dim V（维数公式）	中文：f的核 / 零空间英文：kernel of f / null space
\text{im}(f)（或\text{range}(f)）	线性映射的像（值域）：f(x)的所有取值集合	f(x)=Ax，\text{im}(f)=\{Ax\mid x\in V\}；\text{im}(f)是目标空间的子空间	中文：f的像 / 值域英文：image of f / range of f

四、 数论与组合辅助符号

用于计数、排列组合、数论性质描述，是组合数学与数论的核心辅助工具。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\binom{n}{k}（或C(n,k)）	二项式系数：从n个元素中选k个的组合数	\binom{5}{2}=\frac{5!}{2!3!}=10；(a+b)^n=\sum_{k=0}^n\binom{n}{k}a^{n-k}b^k	中文：n选k / 二项式系数(n,k)英文：binomial coefficient n choose k
P(n,k)（或A(n,k)）	排列数：从n个元素中选k个的排列数	P(5,2)=5\times4=20；P(n,k)=\frac{n!}{(n-k)!}	中文：n选k的排列数英文：permutation of n things taken k at a time
S(n,k)	第二类斯特林数：将n个元素分成k个非空子集的方法数	S(4,2)=7；x^n=\sum_{k=0}^nS(n,k)P(x,k)（斯特林恒等式）	中文：第二类斯特林数(n,k)英文：Stirling numbers of the second kind (n,k)
s(n,k)	第一类斯特林数：将n个元素分成k个非空循环排列的方法数	s(4,2)=11；(x)_n=\sum_{k=0}^n s(n,k)x^k（下降阶乘展开）	中文：第一类斯特林数(n,k)英文：Stirling numbers of the first kind (n,k)
C_n	卡特兰数：组合计数中的重要数列（C_n=\frac{1}{n+1}\binom{2n}{n}）	C_0=1，C_1=1，C_2=2；凸n+2边形三角剖分数为C_n	中文：第n个卡特兰数英文：n-th Catalan number
\gcd(a,b)（或(a,b)）	最大公约数：a与b的最大公共因数	\gcd(12,18)=6；\gcd(p,q)=1（p,q为不同素数）	中文：a和b的最大公约数英文：greatest common divisor of a and b
\text{lcm}(a,b)（或[a,b]）	最小公倍数：a与b的最小公共倍数	\text{lcm}(4,6)=12；$\text{lcm}(a,b)\cdot\gcd(a,b)=	a\cdot b
\phi(n)	欧拉函数：小于n且与n互质的正整数个数	\phi(6)=2（1,5与6互质）；\phi(p^k)=p^k-p^{k-1}（p为素数）	中文：欧拉函数n英文：Euler's totient function of n

五、 拓扑与几何辅助符号

用于空间性质、图形关系的简化描述，辅助拓扑证明与几何计算。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\partial A	边界符号：集合A的边界（闭包减内部）	开区间(0,1)的边界\partial(0,1)=\{0,1\}；圆盘D^2的边界\partial D^2=S^1（圆周）	中文：A的边界英文：boundary of A
\overline{A}（或\text{cl}(A)）	闭包符号：包含A的最小闭集	(0,1)的闭包\overline{(0,1)}=[0,1]；\overline{A}=\text{int}(A)\cup\partial A	中文：A的闭包英文：closure of A
\text{int}(A)（或A^\circ）	内部符号：A中最大的开集	[0,1]的内部\text{int}([0,1])=(0,1)；单点集\{x\}的内部\text{int}(\{x\})=\emptyset	中文：A的内部英文：interior of A
N(x,\epsilon)	ε-邻域：以x为中心、ε为半径的开邻域	平面中N(x,0.5)是以x为中心、半径0.5的开圆盘；拓扑中用于定义连续性	中文：x的ε邻域英文：epsilon-neighborhood of x
\cong（拓扑）	同胚符号：拓扑空间X与Y双向连续同构	圆盘与正方形同胚（D^2\cong[0,1]\times[0,1]）；球面与椭球面同胚	中文：同胚于英文：homeomorphic to
\simeq（同伦）	同伦符号：映射f与g可连续形变互变	恒等映射与常值映射同伦（\text{id}_X\simeq c，X为凸空间）	中文：同伦于英文：homotopic to
d(x,y)	距离函数：两点x,y间的距离	欧氏距离d(x,y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}；离散距离d(x,y)=1（x\neq y）	中文：x和y的距离英文：distance between x and y

六、 概率统计辅助符号

用于分布描述、统计推断的简化表达，辅助概率计算与统计分析。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\chi^2	卡方统计量：拟合优度检验、独立性检验的核心统计量	拟合优度检验\chi^2=\sum\frac{(O-E)^2}{E}（O为观测值，E为期望值）；\chi^2\sim\chi^2(k)（自由度k）	中文：卡方统计量英文：chi-squared statistic
Z（或U）	标准正态统计量：Z=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}	大样本均值检验Z=\frac{175-170}{6/\sqrt{100}}\approx8.33；Z\sim N(0,1)	中文：Z统计量 / U统计量英文：Z-statistic / U-statistic
T	t统计量：小样本均值检验、配对检验的统计量	T=\frac{\overline{X}-\mu}{S/\sqrt{n}}；T\sim t(n-1)（自由度n-1）	中文：t统计量英文：t-statistic
F	F统计量：方差齐性检验、方差分析的统计量	两总体方差检验F=\frac{S_1^2}{S_2^2}；F\sim F(k1,k2)（自由度k1,k2）	中文：F统计量英文：F-statistic
\hat{\theta}	参数估计量：样本构造的总体参数\theta的估计	总体均值\mu的估计量\hat{\mu}=\overline{X}；总体概率p的估计量\hat{p}=\frac{X}{n}	中文：theta的估计量 / theta帽英文：estimator of theta / theta hat
I(X;Y)	互信息：刻画随机变量X与Y的关联程度	$I(X;Y)=H(X)-H(X	Y)（H为熵）；独立变量I(X;Y)=0$
H(X)	熵（香农熵）：描述随机变量的不确定性	二项分布X\sim B(1,p)，H(X)=-p\ln p-(1-p)\ln(1-p)	中文：X的熵英文：entropy of X

七、 补充说明

1. 辅助符号的核心作用：这类符号不直接定义数学概念，而是通过“缩写”“统一格式”简化推导过程（如\delta_{ij}替代复杂的分段表达）、明确上下文关系（如\triangleq区分定义与等式），是数学专业高效沟通的“通用语言”。
2. 易混淆符号区分：
   • \delta_{ij}（克罗内克符号）与\delta(x)（狄拉克函数）：前者是离散指标符号，后者是广义函数，仅符号外形相同；
   • o(g(x))与O(g(x))：小o强调“高阶无穷小”（比值趋于0），大O强调“有界控制”（比值有界）；
   • \cong：几何中表示“全等”，拓扑中表示“同胚”，需结合领域判断含义。
3. 使用规范：辅助符号的含义具有强约定俗成性（如\text{tr}(\mathbf{A})固定表示矩阵的迹），跨领域使用时需明确说明；部分符号有多种写法（如指示函数I_A(x)与\chi_A(x)），可根据研究领域习惯选择。