数学第一章：认识数学符号⑤-特殊常量与变量符号

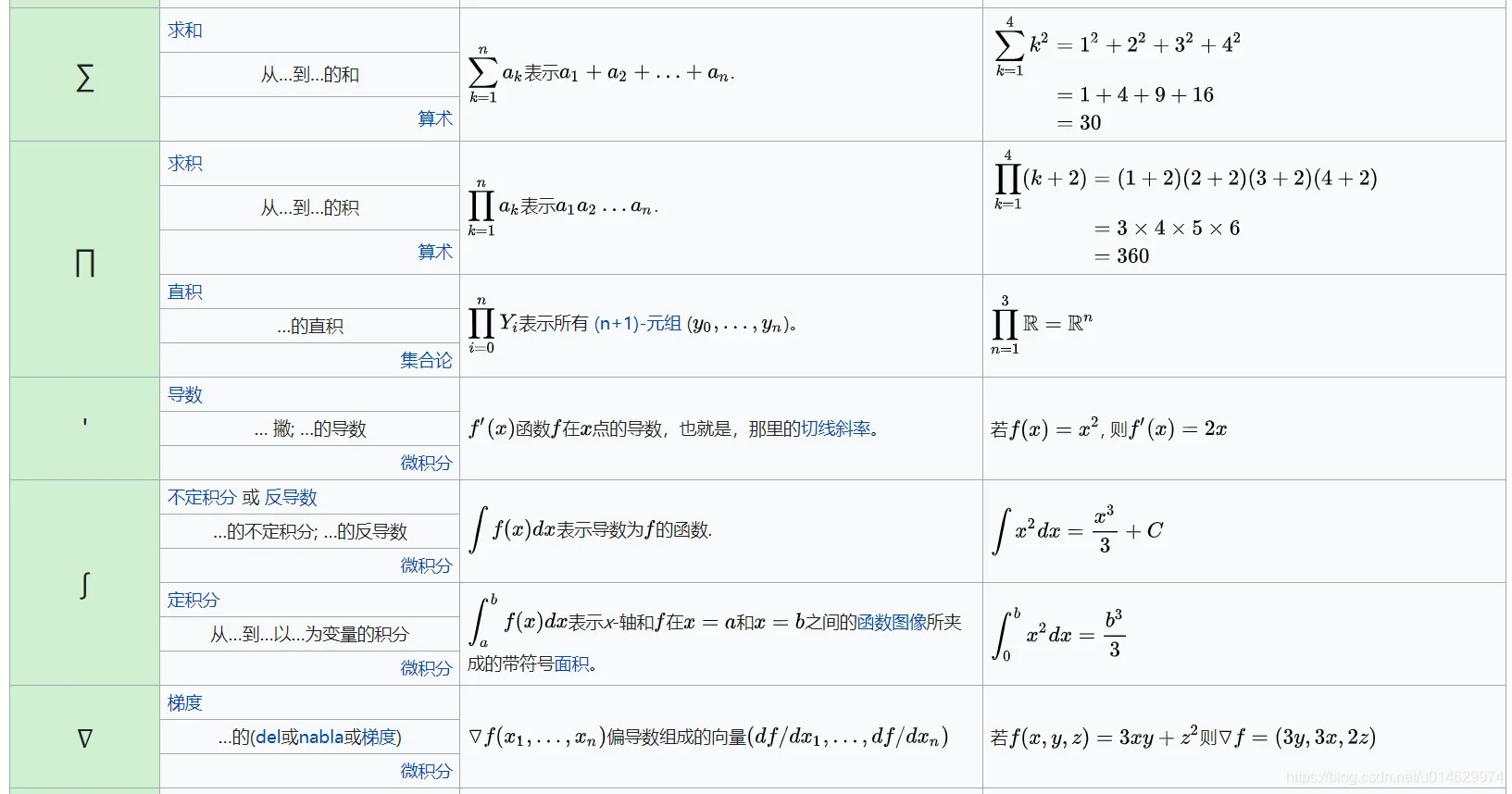
一、 特殊常数（按领域分类）

特殊常数是数学中固定不变、具有特定意义的数值，广泛应用于各分支的公式推导与计算。

符号	数学意义	实用举例	读音（中文+英文常用念法）
\pi（pi）	圆周率（圆的周长与直径的比值，无理数）	圆的周长 C=2\pi r；圆的面积 S=\pi r^2；\pi\approx3.1415926535	中文：圆周率（pài）英文：pi
e（Euler's number）	自然常数（自然指数/对数的底数，无理数）	自然指数函数 y=e^x（导数为自身）；\ln e=1；e\approx2.7182818284	中文：自然常数（yì）英文：Euler's number / e
i（imaginary unit）	虚数单位（满足 i^2=-1，复数的基本组成）	复数 z=a+bi（a,b\in\mathbb{R}）；i^3=-i；i^4=1	中文：虚数单位（ài）英文：imaginary unit / i
\gamma（Euler-Mascheroni constant）	欧拉-马歇罗尼常数（调和级数与自然对数的差值，无理数）	\gamma=\lim\limits_{n\to\infty}\left(1+\frac{1}{2}+\dots+\frac{1}{n}-\ln n\right)；\gamma\approx0.5772156649	中文：欧拉-马歇罗尼常数（yǎ）英文：Euler-Mascheroni constant / gamma
\phi（golden ratio）	黄金比例（满足 \phi=\frac{1+\sqrt{5}}{2}，无理数）	黄金矩形的宽长比为 \frac{1}{\phi}；斐波那契数列极限 \lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}=\phi；\phi\approx1.6180339887	中文：黄金比例（fēi）英文：golden ratio / phi
G（Catalan's constant）	卡塔兰常数（分析与数论中的重要常数，疑似无理数）	G=\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}；G\approx0.9159655942	中文：卡塔兰常数（jiǎ）英文：Catalan's constant / G
K（Khinchin's constant）	辛钦常数（数论中连分数相关常数，无理数）	几乎所有实数的连分数展开中，收敛因子的极限为 K；K\approx2.6854520010	中文：辛钦常数（kǎ）英文：Khinchin's constant / K
\zeta(s)（Riemann zeta function）	黎曼zeta函数（数论核心函数，s 为复数）	\zeta(2)=\sum\limits_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}；\zeta(3) 为阿佩里常数（\approx1.2020569032）	中文：黎曼zeta函数（zī tā）英文：Riemann zeta function
\Gamma(z)（gamma function）	伽马函数（阶乘的推广，z 为复数）	\Gamma(n)=(n-1)!（n\in\mathbb{N}^*）；\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}	中文：伽马函数（gā mǎ）英文：gamma function
\Omega（Chaitin's constant）	蔡廷常数（算法信息论中的不可计算常数）	表示随机生成的程序终止概率，具有不可计算性	中文：蔡廷常数（ōu mì gǎ）英文：Chaitin's constant / Omega
c（speed of light）	真空中的光速（物理常数，数学建模常用）	相对论能量公式 E=mc^2；c\approx2.99792458\times10^8\ \text{m/s}	中文：光速（cè）英文：speed of light / c
\hbar（reduced Planck constant）	约化普朗克常数（量子力学中的数学常数）	角动量量子化公式 L=n\hbar；\hbar=\frac{h}{2\pi}\approx1.054571817\times10^{-34}\ \text{J·s}	中文：约化普朗克常数（h-bar）英文：reduced Planck constant / h-bar

二、 常用变量符号（按领域分类）

变量符号是数学中表示不确定数值、集合、函数等的符号，具有约定俗成的使用场景，便于跨领域交流。

（一）基础通用变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
x, y, z	基础变量（常用于表示未知量、自变量）	方程 $2x+3=7；函数 y=f(x)；三维坐标 (x,y,z)$	中文：变量x、变量y、变量z英文：variable x, variable y, variable z
a, b, c	常数参数（常用于表示固定系数、已知量）	一次函数 y=ax+b；三角形边长 a,b,c	中文：参数a、参数b、参数c英文：parameter a, parameter b, parameter c
m, n, k	整数变量（常用于表示自然数、整数参数）	数列通项 a_n；求和指标 \sum\limits_{k=1}^n k；矩阵行数 m、列数 n	中文：整数m、整数n、整数k英文：integer m, integer n, integer k
t	参数变量（常用于表示时间、参数）	参数方程 \begin{cases}x=\cos t\\y=\sin t\end{cases}；运动方程 s(t)=vt+\frac{1}{2}at^2	中文：参数t英文：parameter t
\varepsilon（epsilon）	小正数变量（常用于极限、连续性定义）	极限定义中“\forall\varepsilon>0,\exists\delta>0”；无穷小量 \varepsilon\to0	中文：小正数ε（ài pǔ sī lóng）英文：epsilon
\delta（delta）	增量/小正数变量（常用于极限、微分定义）	微分中 \Delta x\approx\delta x；极限定义中与 \varepsilon 配套使用	中文：增量δ（dé lǐ tā）英文：delta

（二）数论变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
p, q	素数变量（表示质数，仅能被1和自身整除的整数）	素数分解 $12=2^2\times3$；哥德巴赫猜想“任一偶数可表为两素数和”	中文：素数p、素数q英文：prime number p, prime number q
n!（factorial）	阶乘（n 个正整数的乘积）	$5!=5\times4\times3\times2\times1=120；$0!=1	中文：n的阶乘英文：n factorial
\gcd(a,b)（greatest common divisor）	最大公约数（a 和 b 的最大公共因数）	\gcd(12,18)=6；\gcd(p,q)=1（p,q 为不同素数）	中文：a和b的最大公约数英文：greatest common divisor of a and b
\text{lcm}(a,b)（least common multiple）	最小公倍数（a 和 b 的最小公共倍数）	\text{lcm}(4,6)=12；$\text{lcm}(a,b)\times\gcd(a,b)=	a\times b
\phi(n)（Euler's totient function）	欧拉函数（小于 n 且与 n 互质的正整数个数）	\phi(6)=2（1、5与6互质）；\phi(p)=p-1（p 为素数）	中文：欧拉函数φ(n)（fēi）英文：Euler's totient function of n
\mu(n)（Möbius function）	莫比乌斯函数（数论筛法常用函数）	\mu(1)=1；\mu(p)=-1（p 为素数）；\mu(p^k)=0（k\geq2）	中文：莫比乌斯函数μ(n)（mù bǐ wū sī）英文：Möbius function of n

（三）代数与线性代数变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
\mathbf{A}, \mathbf{B}	矩阵（由数组成的矩形阵列，粗体表示）	2阶矩阵 \mathbf{A}=\begin{pmatrix}1&2\\3&4\end{pmatrix}；单位矩阵 \mathbf{I}	中文：矩阵A、矩阵B英文：matrix A, matrix B
\det(\mathbf{A}) / $	\mathbf{A}	$	矩阵 \mathbf{A} 的行列式（标量值，刻画矩阵性质）
\mathbf{A}^{-1}	矩阵 \mathbf{A} 的逆矩阵（满足 \mathbf{A}\mathbf{A}^{-1}=\mathbf{I}）	\begin{pmatrix}2&1\\1&1\end{pmatrix}^{-1}=\begin{pmatrix}1&-1\\-1&2\end{pmatrix}	中文：矩阵A的逆矩阵英文：inverse of matrix A
\text{tr}(\mathbf{A})（trace）	矩阵 \mathbf{A} 的迹（主对角线元素之和）	\text{tr}\begin{pmatrix}1&2\\3&4\end{pmatrix}=1+4=5；\text{tr}(\mathbf{AB})=\text{tr}(\mathbf{BA})	中文：矩阵A的迹（jī）英文：trace of matrix A
\mathbf{v}, \vec{v}	向量（有大小和方向的量，粗体或带箭头）	列向量 \mathbf{v}=\begin{pmatrix}1\\2\end{pmatrix}；行向量 \vec{v}=(1,2,3)	中文：向量v英文：vector v
V, W	向量空间（线性代数的核心结构，满足线性运算）	实数域上的二维向量空间 \mathbb{R}^2；矩阵构成的向量空间 M_{2\times2}(\mathbb{R})	中文：向量空间V、向量空间W英文：vector space V, vector space W
\lambda（eigenvalue）	特征值（满足 \mathbf{A}\mathbf{v}=\lambda\mathbf{v} 的标量）	矩阵 \begin{pmatrix}2&1\\1&2\end{pmatrix} 的特征值为 1 和 3	中文：特征值λ（lán bā dǎ）英文：eigenvalue / lambda

（四）分析变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
f, g, h	函数符号（表示对应法则）	函数 f(x)=x^2；复合函数 f\circ g(x)=f(g(x))	中文：函数f、函数g英文：function f, function g
u(x,y), v(x,y)	多元函数（依赖多个自变量的函数）	二元函数 u(x,y)=x^2+y^2；调和函数 \Delta u=0	中文：多元函数u、多元函数v英文：multivariate function u, multivariate function v
\omega（angular frequency）	角频率（分析振动、波动常用变量）	简谐运动 x=A\sin(\omega t+\phi)；\omega=2\pi f（f 为频率）	中文：角频率ω（ōu mì gǎ）英文：angular frequency / omega
L（operator）	线性算子（分析中表示变换的符号）	微分算子 L=\frac{d}{dx}；拉普拉斯算子 L=\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}	中文：线性算子L英文：linear operator L

（五）几何与拓扑变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
\theta, \alpha, \beta	角度变量（表示几何中的角）	三角函数 \sin\theta；直线与平面的夹角 \alpha	中文：角θ（θ读sāi tā）、角α（ā lā fǎ）、角β（bēi tǎ）英文：angle theta, angle alpha, angle beta
r	半径变量（圆、球等图形的半径）	圆的面积 S=\pi r^2；球的体积 V=\frac{4}{3}\pi r^3	中文：半径r英文：radius r
s	弧长变量（曲线、圆弧的长度）	圆的弧长 s=r\theta（\theta 为弧度）；曲线积分 \int_L f ds	中文：弧长s英文：arc length s
d	距离变量（点、线、面之间的距离）	两点间距离 d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}；点到直线的距离	中文：距离d英文：distance d
V	体积变量（几何体所占空间的大小）	长方体体积 V=abc；柱体体积 V=Sh（S 为底面积，h 为高）	中文：体积V英文：volume V

（六）概率统计变量

符号	数学意义	实用举例	读音（中文+英文常用念法）
X, Y, Z	随机变量（表示随机试验结果的变量）	离散随机变量 X（掷骰子的点数）；连续随机变量 Y（身高）	中文：随机变量X、随机变量Y英文：random variable X, random variable Y
P(A)	事件 A 的概率（事件发生的可能性大小）	掷骰子出现偶数的概率 P(A)=\frac{1}{2}；概率公理 $0\leq P(A)\leq1$	中文：事件A的概率英文：probability of event A
\mu（mean）	均值（随机变量的平均取值，期望）	正态分布的均值 \mu；样本均值 \bar{X}=\frac{1}{n}\sum\limits_{i=1}^n X_i	中文：均值μ（mù）英文：mean / mu
\sigma（standard deviation）	标准差（刻画数据的离散程度）	方差 \sigma^2=E[(X-\mu)^2]；标准差 \sigma=\sqrt{\sigma^2}	中文：标准差σ（sī gǎ mǎ）英文：standard deviation / sigma
\rho（correlation coefficient）	相关系数（刻画两个变量的线性相关程度）	相关系数 \rho\in[-1,1]；\rho=1 表示完全正相关	中文：相关系数ρ（ròu）英文：correlation coefficient / rho
N(\mu,\sigma^2)	正态分布（连续型概率分布，又称高斯分布）	标准正态分布 N(0,1)；身高、体重常服从正态分布	中文：均值为μ、方差为σ²的正态分布英文：normal distribution with mean mu and variance sigma squared
f(x)（probability density function）	概率密度函数（连续随机变量的分布密度）	标准正态分布的密度函数 f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}	中文：概率密度函数f(x)英文：probability density function f(x)

三、 补充说明

1. 常数的通用性：部分常数跨领域使用（如 \pi 同时用于几何、分析、概率），其意义保持一致，仅应用场景不同。
2. 变量的约定俗成：变量符号的使用具有习惯性（如 p 通常表示素数、\theta 表示角度），避免随意替换可提高可读性。
3. 易混淆符号区分：
   • 黄金比例 \phi 与欧拉函数 \phi(n)：符号相同但领域不同，需结合上下文判断；
   • 均值 \mu 与莫比乌斯函数 \mu(n)：读音相同（中文均读mù），但意义完全不同，依赖符号位置（函数后带参数，均值为单独符号）区分。
4. 常数近似值：表中给出常用常数的10位近似值，满足大部分计算需求（高精度计算需参考专门数据表）。