数学第一章：认识数学符号④-几何和拓扑符号

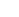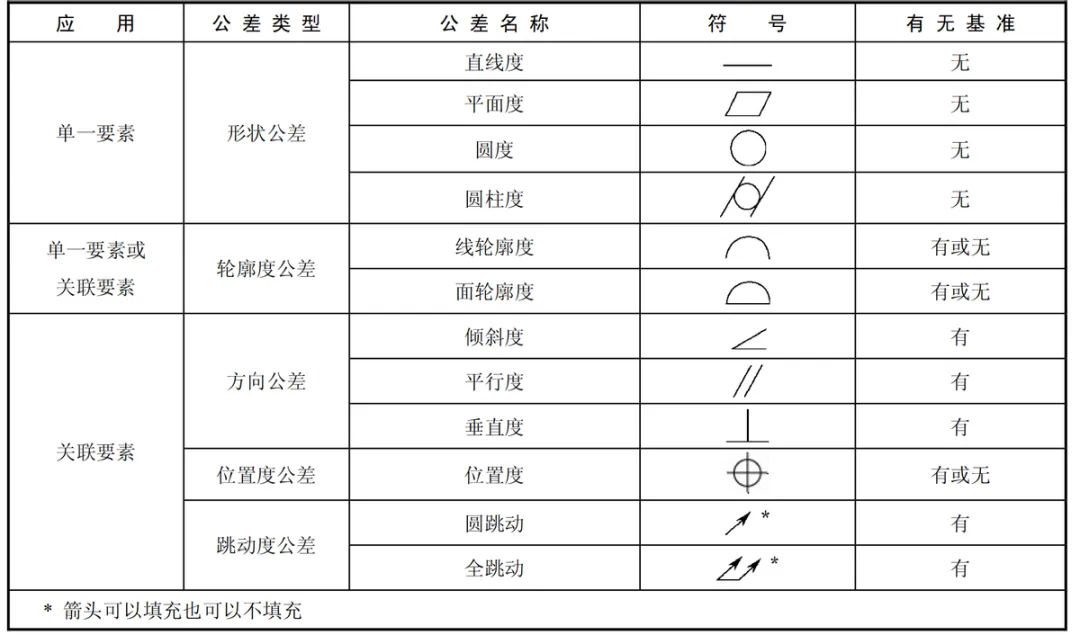
一、 几何基础符号（平面/欧式几何）

符号	数学意义	实用举例	读音（中文+英文常用念法）
A, B, C\dots	点（几何中的基本元素）	平面上有三点A(1,2)、B(3,4)、C(5,6)	中文：点A、点B英文：point A, point B
直线AB / l	过两点A、B的直线，l为直线的简化表示	直线AB垂直于直线CD；直线l的方程为y=2x+1	中文：直线AB、直线l英文：line AB, line l
线段AB	A、B两点间的有限部分（含端点）	线段AB的长度为5；线段AB的中点为M	中文：线段AB英文：line segment AB
射线AB	以A为端点，向B方向无限延伸的线	射线AB与射线AC组成\angle BAC	中文：射线AB英文：ray AB
\angle ABC	由射线BA、BC组成的角，顶点为B	\angle ABC=60^\circ（锐角）；\angle AOB为圆心角（O为圆心）	中文：角ABC英文：angle ABC
\perp	垂直关系（直线与直线、直线与平面等）	直线l\perp直线m；AB\perp平面\alpha	中文：垂直于英文：perpendicular to
\parallel	平行关系（直线与直线、平面与平面等）	直线AB\parallel直线CD；平面\alpha\parallel平面\beta	中文：平行于英文：parallel to
\cong	全等（图形形状和大小完全相同）	\triangle ABC\cong\triangle DEF（全等三角形）；圆O_1\cong圆O_2	中文：全等于英文：congruent to
\sim	相似（图形形状相同，大小成比例）	\triangle ABC\sim\triangle DEF（相似比为$2:1$）；相似多边形	中文：相似于英文：similar to
\odot O	以O为圆心的圆	\odot O的半径为3；AB是\odot O的直径	中文：圆O英文：circle O
\overset{\frown}{AB}	圆上A、B两点间的弧（简记为弧AB）	\overset{\frown}{AB}为优弧（大于半圆）；\overset{\frown}{CD}为劣弧（小于半圆）	中文：弧AB英文：arc AB
d(A,B)	两点A、B间的距离	d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}（平面直角坐标下）	中文：A、B两点间的距离英文：distance between A and B

二、 向量与解析几何符号

符号	数学意义	实用举例	读音（中文+英文常用念法）
\vec{a} / \vec{AB}	向量（有大小和方向的量），\vec{AB} 表示从A到B的向量	\vec{a}=(1,2)（二维向量）；\vec{AB}=\vec{OB}-\vec{OA}	中文：向量a、向量AB英文：vector a, vector AB
|\vec{a}|	向量\vec{a}的模（长度）	|\vec{a}|=5（向量a的长度为5）；|(3,4)|=5	中文：向量a的模英文：magnitude of vector a、norm of vector a
\vec{a}\cdot\vec{b}	向量\vec{a}与\vec{b}的点积（内积、数量积）	\vec{a}=(1,2), \vec{b}=(3,4)，则\vec{a}\cdot\vec{b}=1\times3+2\times4=11	中文：向量a点乘向量b英文：dot product of vector a and vector b
\vec{a}\times\vec{b}	向量\vec{a}与\vec{b}的叉积（外积、向量积）	\vec{a}=(1,0,0), \vec{b}=(0,1,0)，则\vec{a}\times\vec{b}=(0,0,1)	中文：向量a叉乘向量b英文：cross product of vector a and vector b
\vec{e}	单位向量（模为1的向量）	x轴方向单位向量\vec{e}_x=(1,0)；\vec{a}=|\vec{a}|\vec{e}_a	中文：单位向量e英文：unit vector e
\nabla	nabla算子（哈密顿算子，用于梯度、散度、旋度）	\nabla f为函数f的梯度；\nabla\cdot\vec{a}为向量\vec{a}的散度	中文：纳布拉算子英文：nabla operator、Hamiltonian operator
(x,y,z)	空间直角坐标系中的点坐标	点P(1,2,3)在第一卦限；点O(0,0,0)为坐标原点	中文：x,y,z坐标英文：x y z coordinates
Ax+By+Cz+D=0	空间平面的一般式方程	平面x+y+z-1=0过点(1,0,0)、(0,1,0)、(0,0,1)	中文：空间平面一般式方程英文：general equation of a spatial plane
\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}	空间直线的对称式方程（方向向量为(l,m,n)）	直线\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}过点(1,2,3)，方向向量(2,3,4)	中文：空间直线对称式方程英文：symmetric equation of a spatial line

三、 立体几何符号

符号	数学意义	实用举例	读音（中文+英文常用念法）
\alpha, \beta, \gamma\dots	平面（立体几何中的二维平面元素）	平面\alpha与平面\beta的交线为直线l；直线l在平面\alpha内（l\subset\alpha）	中文：平面α、平面β英文：plane α, plane β
l\subset\alpha	直线l在平面\alpha内	若直线l\subset\alpha，点A\in l，则A\in\alpha	中文：直线l包含于平面α英文：line l is contained in plane α
\alpha\cap\beta=l	平面\alpha与平面\beta的交线为直线l	平面xOy（z=0）与平面xOz（y=0）的交线为x轴（l:x轴）	中文：平面α与平面β相交于直线l英文：plane α intersects plane β at line l
\theta（二面角）	两个平面（或直线与平面）的夹角	平面\alpha与平面\beta的二面角\theta=60^\circ；直线l与平面\alpha的夹角为$30^\circ$	中文：二面角θ、线面角θ英文：dihedral angle θ, line-plane angle θ
V	几何体的体积	正方体体积V=a^3（a为棱长）；球体体积V=\frac{4}{3}\pi r^3	中文：体积英文：volume
S	几何体的表面积（或平面图形的面积）	球体表面积S=4\pi r^2；长方体表面积S=2(ab+bc+ac)	中文：表面积、面积英文：surface area, area
\square	平行六面体（由六个平行四边形围成的几何体）	长方体是特殊的平行六面体（六个面为矩形）	中文：平行六面体英文：parallelepiped
棱锥/棱台	棱锥：底面为多边形，侧面为三角形的几何体；棱台：棱锥截去顶部后的几何体	正四棱锥（底面为正方形，顶点在底面投影为中心）；正四棱台	中文：棱锥、棱台英文：pyramid, frustum of a pyramid

四、 拓扑基础符号

符号	数学意义	实用举例	读音（中文+英文常用念法）
X, Y	拓扑空间（非空集合X与其上的拓扑结构组成）	X=\mathbb{R}（实数集），赋予通常拓扑，成为拓扑空间(\mathbb{R}, \tau)	中文：拓扑空间X、拓扑空间Y英文：topological space X, topological space Y
\tau（tau）	拓扑（X的子集族，满足闭包、并、有限交公理）	$\tau={\emptyset, \mathbb{R}, (a,b)\mid\forall a英文：topology τ, tau
U, V	开集（拓扑\tau中的元素）	在通常拓扑下，(0,1)是\mathbb{R}上的开集；\emptyset和\mathbb{R}是平凡拓扑的仅有的开集	中文：开集U、开集V英文：open set U, open set V
\overline{A}	集合A的闭包（包含A的最小闭集）	A=(0,1)\subset\mathbb{R}，\overline{A}=[0,1]（闭区间）；A=\{1/n\mid n\in\mathbb{N}\}，\overline{A}=A\cup\{0\}	中文：A的闭包英文：closure of A
\text{int}(A) / \mathring{A}	集合A的内部（A中最大的开集）	A=[0,1]\subset\mathbb{R}，\text{int}(A)=(0,1)；A=\{0\}，\text{int}(A)=\emptyset	中文：A的内部英文：interior of A
\partial A	集合A的边界（闭包减去内部）	A=(0,1)\subset\mathbb{R}，\partial A=\{0,1\}；A=\mathbb{R}^2（平面），\partial A=\emptyset	中文：A的边界英文：boundary of A
A^\circ	同\text{int}(A)，集合A的内部	A=[1,2]，A^\circ=(1,2)	中文：A的内部英文：interior of A
N(x, \varepsilon)	点x的\varepsilon-邻域（以x为中心，\varepsilon为半径的开集）	在\mathbb{R}^2中，N(x, 0.5)是以x为中心、半径0.5的开圆盘	中文：x的ε邻域英文：epsilon-neighborhood of x
x\in\overline{A}	点x是集合A的聚点（极限点）	$0$是A=\{1/n\mid n\in\mathbb{N}\}的聚点；(0,1)内的点都是自身的聚点	中文：x是A的聚点英文：x is a limit point of A

五、 拓扑空间与映射符号

符号	数学意义	实用举例	读音（中文+英文常用念法）
f: X\to Y 连续	拓扑空间X到Y的连续映射（开集的原像是开集）	f: \mathbb{R}\to\mathbb{R}, f(x)=x^2是连续映射；常值映射f(x)=c（c为常数）是连续映射	中文：f是从X到Y的连续映射英文：f is a continuous map from X to Y
X\cong Y（拓扑同胚）	X与Y同胚（存在双向连续的一一映射）	圆盘与正方形同胚；球面与椭球面同胚	中文：X同胚于Y英文：X is homeomorphic to Y
X\approx Y	同X\cong Y，拓扑空间X与Y同胚	线段[0,1]与线段[2,3]同胚（X\approx Y）	中文：X同胚于Y英文：X is homeomorphic to Y
f: X\to Y 同胚	f是X到Y的同胚映射（连续、双射、逆映射连续）	f(x)=x+1: [0,1]\to[1,2]是同胚映射	中文：f是从X到Y的同胚映射英文：f is a homeomorphism from X to Y
X\times Y	拓扑空间X与Y的积空间（拓扑由乘积拓扑生成）	\mathbb{R}\times\mathbb{R}=\mathbb{R}^2（平面），乘积拓扑为平面通常拓扑；S^1\times S^1=T^2（环面）	中文：X与Y的积空间英文：product space of X and Y
X/Y	拓扑空间X模去子集Y的商空间（将Y中所有点等同为一点）	\mathbb{R}/[0,1]（将线段[0,1]捏合成一点）；S^1/\{p\}=S^1（球面模去一点同胚于球面）	中文：X模Y的商空间英文：quotient space of X by Y
i: A\to X	包含映射（A是X的子空间，i(a)=a\ \forall a\in A）	A=[0,1]\subset\mathbb{R}，i: [0,1]\to\mathbb{R}, i(x)=x是包含映射	中文：i是从A到X的包含映射英文：i is the inclusion map from A to X

六、 同伦与同调相关符号

符号	数学意义	实用举例	读音（中文+英文常用念法）
f\simeq g	映射f与g同伦（存在连续形变将f变为g）	f(x)=x与g(x)=0: \mathbb{R}\to\mathbb{R}同伦（H(t,x)=x(1-t)为同伦）	中文：f同伦于g英文：f is homotopic to g
H: X\times I\to Y	同伦H（I=[0,1]，H(\cdot,0)=f, H(\cdot,1)=g）	H(t,x)=(x_1\cos\pi t - x_2\sin\pi t, x_1\sin\pi t + x_2\cos\pi t)是\mathbb{R}^2上恒等映射到旋转映射的同伦	中文：同伦H英文：homotopy H
\pi_n(X, x_0)	n维同伦群（X在基点x_0处的n维环路同伦类构成的群）	\pi_1(S^1, x_0)=\mathbb{Z}（圆周的一维同伦群为整数群）；\pi_n(S^1, x_0)=0（n\geq2）	中文：X在x₀处的n维同伦群英文：n-th homotopy group of X at base point x₀
H_n(X)	n维奇异同调群（拓扑空间X的n维同调群，刻画孔洞数量）	H_0(S^1)=\mathbb{Z}（圆周的0维同调群）；H_1(S^1)=\mathbb{Z}；H_n(S^1)=0（n\geq2）	中文：X的n维同调群英文：n-th singular homology group of X
S^n	n维球面（n维欧氏空间中到原点距离为1的点集）	S^1为圆周（1维球面）；S^2为通常球面（2维球面）；S^0为两点集\{\pm1\}	中文：n维球面英文：n-sphere
D^n	n维圆盘（n维欧氏空间中到原点距离≤1的点集）	D^1=[-1,1]（1维圆盘，线段）；D^2为闭圆盘（2维圆盘）	中文：n维圆盘英文：n-disk、n-ball
\partial D^n=S^{n-1}	n维圆盘的边界是n-1维球面	\partial D^2=S^1（2维圆盘的边界是圆周）；\partial D^1=S^0（1维圆盘的边界是两点）	中文：n维圆盘的边界是n-1维球面英文：the boundary of n-disk is n-1-sphere

七、 补充说明

1. 几何符号的适用场景：平面几何符号多用于基础图形关系（平行、垂直、全等），解析几何符号侧重坐标与向量运算，立体几何符号聚焦空间几何体的位置与度量关系。
2. 拓扑符号的核心逻辑：拓扑关注空间的“连续不变性”，同胚、同伦、同调等符号均服务于刻画空间在连续形变下不变的性质（如孔洞数量、连通性）。
3. 易混淆符号区分：① 几何中的“\cong”（全等）与拓扑中的“\cong”（同胚）：全等要求形状和大小完全一致，同胚仅要求连续形变可互变（如圆盘与正方形同胚但不全等）；② 边界符号“\partial”：几何中边界是图形的边缘（如线段的端点），拓扑中边界是闭包减内部（如开区间的边界是端点）。